宜兴教育云

从三角形内角和到多边形内角和实践探究

•   四年级上册数学我们学习了角的度量，通过测量各种不同形状三角形的内角，随着图形形状的变化，各个内角的度数也随之改变，但是三角形的内角和都是180°，我不禁产生了疑问，任意三角形的内角和都是一个固定值吗？那四边形，五边形，六边形，任意多边形的内角和呢？

探究过程

• 一、探究工具        剪刀、若干A4纸、量角器、铅笔、直尺

• 二、探究过程

1、探究探究三角形里的小秘密     

我们在A4纸上画了3个不同形状的三角形（直角三角形、锐角三角形、钝角三角形），用量角器分别测出它们内角的度数。如图（1）：90°+40°+50°=180°，如图（2）：118°+33°+29°=180°，如图（3）：57°+65°+58°=180°。

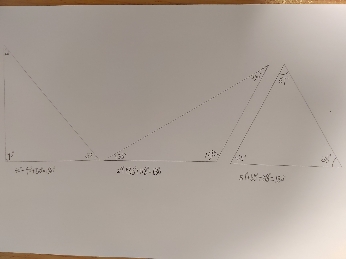
继续设计探究实验——剪一剪、拼一拼。画三个不同形状的三角形，用剪刀将其三个内角分别剪下来，拼一拼，均拼出了平角（如图4），证实了三角形的内角和是180°。

还可以折一折，如图（5），三个内角构成一个平角。我们发现了三角形里的小秘密——三个内角和是180°。

2、借力三角形探究四边形内角和 

  四边形的内角和会是一个固定值吗？通过测量和拼角的方法猜测四边形的内角和是360°。为了进一步验证实验结果准确性，我想到了数学老师常常教导我们的一句话：“遇到不会的知识要想办法转化成学过的知识去解决。”何不将求四边形内角和问题转化成求三角形内角和问题呢？

（1）     锦囊妙计

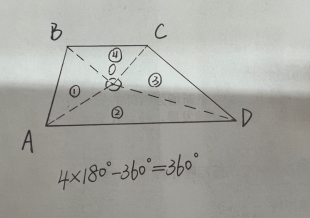
方法1：如图（6），在四边形内任取一点O，连接OA,OB,OC,OD。则四边形被分成了4个三角形。这4个三角形的内角和是4ⅹ180°，以O为公共点的4个角的和是360°，所以四边形的内角和是4ⅹ180°-360°=360°。

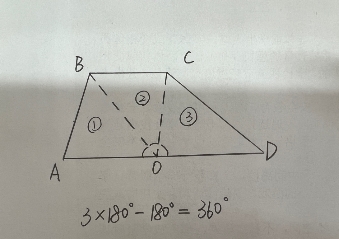
方法2：如图（7），在四边形边AD上取一点O，连接OB、OC。则四边形被分成了3个三角形, 这3个三角形的内角和为3×180°, 以0为公共顶点的3个角的和是180°，所以四边形的内角和是3×180°-180°=360°。

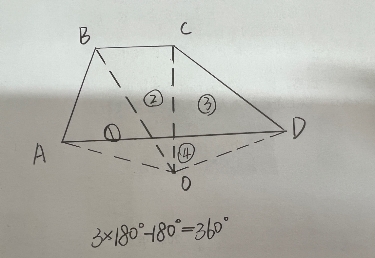
方法3：如图（9），在四边形外取一点O，连接OA、OB、OC、OD。则四边形被分成了3个三角形。以O,A,D为顶点的三角形的三个内角正好是多余部分。所以四边形的内角和是3ⅹ180°-180°=360°。

方法4：如图（8），连接对角线AC。则四边形被分成了2个三角形, 这2个三角形的内角和为2×180°=360°。

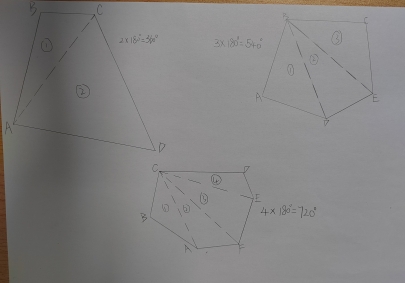
通过以上方法都说明了四边形的内角和等于360°。

（2）对比研究     

  条条道路通罗马，到底哪条路是捷径呢？对比以上4种方法都有一个共同的特点，将探究四边形的内角和转化成三角形内角和知识来解决。细品其中的过程，很明显从一个顶点出发构造三角形是最简便的做法，即方法4。方法4的优点是没有多余角产生，简洁明了。

3、深入五边形、六边形——多边形内角和迎刃而解。

• 三、实验结论     

• 通过研究，原来多边形的内角和与它的边数有关系。如果一个多边形有n条边，那么它的内角和就是180°×（n-2)。    用发现的眼睛看数学，用探究的精神学数学，数学知识变得那么有趣、简单。本次探究活动，更加坚定了我学好数学的决心，原来小头脑也有大风暴。

原作者：桃溪小学四年级组